코사인 유사도(Cosine Similarity)의 개념과 원리를 간단히 정리하고 간단한 파이썬 예제를 살펴봅니다.

.

본 포스트는 클로드의 도움을 받아 작성되었습니다.

.

2026. 2. 11 최초작성

.

코사인 유사도의 개념과 원리

코사인 유사도란 무엇인가

수학적 근거: 내적(Dot Product)

내적이 유사도를 측정할 수 있는 이유

왜 크기로 나누는가

코사인 유사도 vs 유클리드 거리

왜 비슷한 문장이 같은 방향의 벡터가 되는가

임베딩 모델

방법 1: 직접 세는 방식 (GloVe)

방법 2: 예측하는 방식 (Word2Vec)

벡터 수치가 비슷해지는 과정

Python 예제 코드

.

코사인 유사도의 개념과 원리

코사인 유사도란 무엇인가

Cosine Similarity(코사인 유사도)는 두 벡터 사이의 각도의 코사인 값을 이용해 유사도를 측정하는 방법입니다. 벡터의 크기(magnitude)는 무시하고, 오직 방향(direction)만으로 유사성을 판단합니다.

.

코사인의 유사도의 값 범위는  -1에서 1 사이이며, 각 값의 의미는 아래 표와 같습니다.

값	의미	설명
1	완전히 같은 방향	두 벡터가 완전히 유사함
0	직교 (직각)	두 벡터가 아무 관련 없음
-1	완전히 반대 방향	두 벡터가 완전히 반대됨

.

코사인 유사도의 공식은 다음과 같습니다. 

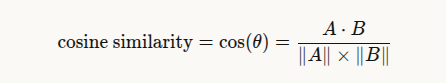
식의 분자는 두 벡터의 내적으로 방향이 얼마나 일치하는 지를 의미하며

분모는 각 벡터의 크기의 곱으로 벡터 크기를 정규화하여 벡터의 크기 영향을 줄이고 벡터의 방향만 비교하도록 합니다.

.

수학적 근거: 내적(Dot Product)

코사인 유사도의 수학적 근거는 내적(dot product)입니다. 

.

내적이 유사도를 측정할 수 있는 이유

내적은 벡터에서 같은 위치의 숫자끼리 곱해서 더하는 연산입니다.  예를 들어 A = [3, 0]과 B = [2, 2]의 내적은 다음과 같이 계산합니다. 

A · B = (3×2) + (0×2) = 6

벡터 A의 첫 번째 값이 3이고 벡터 B의 첫 번째 값이 2이므로 두 값을 곱하면 6이 되지만 A의 두번째 값은 0이고 B의 두번째 값은 2라서 두 값을 곱하면 0이 됩니다. 

즉, 내적은 두 벡터가 같은 위치에 큰값을 가질 수록 값이 커지는 연산입니다.  같은 곳의 값이 클수록 커진다는 것은 같은 특성을 공유함을 의미합니다.

.

왜 크기로 나누는가

내적만 쓰면 문제가 있습니다. 예를 들어  A = [3, 0]과 C = [300, 0]의 내적은 900으로 엄청 크지만, 이건 두 벡터가 유사해서 큰값을 가지는 게 아니라 C의 크기가 크기 때문입니다.  그래서 코사인 유사도에서는 각 벡터의 크기의 영향을 줄이기 위해 각 벡터의 크기로 나누어 정규화를 하게 됩니다.  코사인 유사도에서는 벡터 크기의 영향을 제거하고 벡터의 방향만 따져서 순수하게 “같은 곳에서 함께 큰가”만 봅니다. .

.

코사인 유사도 vs 유클리드 거리

코사인 유사도는 벡터의 크기를 무시하고  두 벡터의 방향이 일치하는지를 중요시하는 반면 유클리드 거리는 벡터의 크기 자체가 중요한 경우 사용됩니다. ( 물리적 좌표간 실제 거리를 측정)

.

코사인 유사도를 텍스트에 적용하면  “고양이가 좋다”라는 짧은 문장과 “고양이는 정말 귀엽고 사랑스러운 동물이라서 너무 좋다”라는 긴 문장이 있을 때, 단어 수(벡터의 크기)는 다르지만 의미의 방향은 고양이에 대해 얘기하고 있어 비슷합니다. 코사인 유사도는 이런 경우 두 문장이 비슷하다고 합니다. 이래서 의미를 중요시하는 경우 방향만 보는 코사인 유사도를 사용합니다.

.

“고양이”, “강아지”, “주식”이라는 3개의 단어가 있을때 다음 세 문장이 각 단어와 연관성을 점수로 매겨봅니다.

문장A: “고양이는 귀여운 동물이다” → 고양이 5, 강아지 0, 주식 0

문장B: “고양이와 강아지는 귀엽다” → 고양이 3, 강아지 3, 주식 0

문장C: “오늘 주식이 폭락했다” → 고양이 0, 강아지 0, 주식 5

이 숫자들이 바로 벡터입니다. A는 [5, 0, 0], B는 [3, 3, 0], C는 [0, 0, 5]가 됩니다. 

이걸 좌표 위에 점으로 찍으면, 원점에서 각 점을 향해 화살표를 그릴 수 있습니다. A와 B의 화살표는 비슷한 쪽(동물 쪽)을 가리키고, C의 화살표는 전혀 다른 쪽(주식 쪽)을 가리킵니다.

코사인 유사도는 이 화살표 사이의 각도를 재는 것입니다. A와 B는 각도가 좁으니까 “비슷하다”, A와 C는 각도가 90도니까 “관련 없다”가 되는 겁니다.

정리하면, 비슷한 주제를 다루는 문장들은 숫자로 바꿨을 때 자연스럽게 비슷한 방향의 벡터가 되고, 그래서 방향(각도)을 비교하는 것이 곧 의미를 비교하는 것이 됩니다.

.

비슷한 문장의 벡터가 같은 방향을 가리키는 이유는, AI가 그렇게 되도록 훈련받았기 때문입니다.

과정을 설명하면 이렇습니다. 임베딩 모델을 훈련시킬 때, “고양이는 귀엽다”와 “고양이는 사랑스럽다”처럼 의미가 비슷한 문장 쌍을 주고 “이 둘의 벡터를 가까운 방향으로 만들어”라고 시킵니다. 반대로 “고양이는 귀엽다”와 “주식이 폭락했다”처럼 관련 없는 문장 쌍을 주고 “이 둘의 벡터를 먼 방향으로 만들어”라고 시킵니다. 이걸 수억 개의 문장 쌍으로 반복하면, 모델이 알아서 의미가 비슷한 문장은 비슷한 방향의 벡터로, 다른 문장은 다른 방향의 벡터로 변환하는 법을 배우게 됩니다.

즉, 코사인 유사도라는 측정 도구를 사용하여 임베딩 모델이 “의미가 비슷한 문장은 코사인 유사도가 높게 나오도록” 벡터를 만들어내는 법을 학습한 것입니다

벡터의 방향이 의미를 담고 있는 게 아니라, 의미가 비슷하면 방향이 비슷해지도록 모델이 설계된 것입니다. 코사인 유사도라는 도구가 먼저 있고, 그 도구에 맞춰서 벡터를 만드는 겁니다.

.

왜 비슷한 문장이 같은 방향의 벡터가 되는가

왜 비슷한 문장이 같은 방향의 벡터가 되는가의 출발점은 분포 가설(Distributional Hypothesis)입니다.

1954년 언어학자 Zellig Harris가 제안하고, 1957년 J.R. Firth가 대중화한 이론 ACL Member Portal으로, 핵심 문장은 이겁니다:

“You shall know a word by the company it keeps” (단어는 함께 쓰이는 동료들로 알 수 있다)

같은 맥락(context)에서 등장하는 단어들은 비슷한 의미를 가진다는 것입니다.

.

“she eats ___ for breakfast”라는 문장의 빈칸에 “apple”과 “banana”는 둘 다 들어갈 수 있지만, “bus”는 들어갈 수 없습니다. 즉 같은 빈칸을 채울 수 있는 단어들은 의미가 비슷합니다.

이것은 아이들이 언어를 배우는 방식과 같습니다. 아이들은 사전을 찾아보지 않고, 단어가 사용되는 맥락을 관찰하면서 의미를 파악합니다. “dog”는 “bark”, “leash”, “pet”, “walk” 근처에서 등장하고, “cat”는 “meow”, “purr”, “pet”, “scratch” 근처에서 등장합니다. 이 패턴을 통해 “dog”과 “cat”이 관련 있다는 것(둘 다 반려동물)을 배우게 됩니다. 

.

이것이 벡터와 어떻게 연결되는가

Word2Vec 같은 모델의 기본 아이디어는, 의미가 비슷한 단어는 비슷한 맥락에서 사용되고, 비슷한 맥락에서 사용되는 단어는 비슷한 의미를 가진다는 것입니다

.

구체적으로 이렇게 작동합니다:

모델이 거대한 텍스트 데이터에서 “각 단어가 어떤 단어들과 함께 등장하는지” 통계를 수집합니다

“the cat sat on the mat”이라는 문장에서 윈도우 크기 3이면 ‘the’, ‘cat’, ‘sat’이 함께 묶이고, 훈련 과정에서 이 단어들의 벡터가 서로 가까워지도록 조정됩니다 

“dog”과 “cat”은 “pet”, “feed”, “cute” 같은 비슷한 주변 단어들과 함께 등장하므로, 훈련이 반복되면서 자연스럽게 비슷한 벡터를 갖게 됩니다

.

그래서 “방향이 같다”는 건 벡터의 각 차원은 특정한 의미적 특성을 나타냅니다. 이런 방식으로 학습된 임베딩은 벡터 연산도 가능한데, 유명한 예시가 king – man + woman ≈ queen입니다. “왕”에서 “남성” 성분을 빼고 “여성” 성분을 더하면 “여왕”이 되는 거죠.

비슷한 맥락에서 등장하는 단어들은 같은 차원에서 비슷한 값을 가지게 되고, 그 결과 벡터가 같은 방향을 가리키게 됩니다.

.

임베딩 모델

그런데 코사인 유사도가 높다고 해서 두 텍스트가 정말 의미적으로 비슷한 걸까요? 이건 벡터 공간이 애초에 의미를 잘 담고 있을 때만 성립합니다. 임베딩의 핵심 아이디어는, 두 텍스트가 비슷하면 그 벡터 표현도 비슷해야 한다는 것이고, 이건 자연스럽게 그렇게 되는 게 아니라 분포 가설이라는 언어학적 근거 위에 모델을 훈련시킨 결과입니다.

그렇다면 이 훈련은 누가 하는 걸까요? “비슷한 의미는 가깝게, 다른 의미는 멀게” — 이런 벡터 공간을 실제로 만들어내는 것이 바로 임베딩 모델의 역할입니다.

.

실제 임베딩 모델이 벡터를 만드는 방법은 크게 두 가지가 있습니다. 

.

방법 1: 직접 세는 방식 (GloVe)

실제로 단어가 동시에 등장 횟수를 세서 거대한 표를 만듭니다. 그 표를 수학적으로 압축해서 벡터를 만드는 방식입니다.  각 축이 특정 단어와 함께 등장한 횟수이므로 직관적이지만, 어휘가 10만 개면 10만 차원이 되어 비효율적입니다.

예를 들어 어휘가 “귀엽다, 먹다, 산책, 투자” 4개면 축이 4개이고, 각 축이 그 단어와 함께 등장한 횟수입니다. 

.

방법 2: 예측하는 방식 (Word2Vec)

빈도를 직접 세지 않고, 대신 “빈칸 맞추기” 문제를 풀게 합니다. 

예시: “우리집 ___ 가 사료를 먹었다”모델에게 “우리집”, “가”, “사료를”, “먹었다”를 주고 빈칸에 뭘가 들어갈지 맞춰보라고 시킨다.정답이 “고양이”인 경우 정답을 알려주고, 벡터를 조금 조정합니다.

예를 들어 384차원 벡터를 만든다고 하면, 이 384개의 축은 특정 단어가 아닙니다. 학습 과정에서 모델이 스스로 만들어낸 추상적인 의미 특성입니다. 단어를 예측하고, 틀리면 벡터 수치를 조정한다”는 과정이 명확하지만 학습이 끝난 후 384개 축 각각이 어떤 의미 특성을 담당하는지를 사람이 해석하기 어렵습니다.

.

벡터 수치가 비슷해지는 과정

.

처음에 모든 단어의 벡터는 랜덤한 숫자입니다.

.

고양이 → [0.12, -0.45, 0.78]  (랜덤)

강아지 → [-0.91, 0.33, 0.05]  (랜덤)

.

이제 모델이 이런 문제를 풀어봅니다:

.

문제 1: “우리집 ___ 가 사료를 먹었다” → 정답: 고양이

.

모델이 틀리면, “고양이” 벡터를 “사료”, “먹었다”의 벡터와 가까워지도록 숫자를 살짝 조정합니다. 예를 들어 0.12를 0.15로, -0.45를 -0.40으로 이런 식으로요.

.

문제 2: “우리집 ___ 가 사료를 먹었다” → 정답: 강아지

.

이번엔 “강아지” 벡터를 “사료”, “먹었다”의 벡터와 가까워지도록 조정합니다.

.

여기서 핵심이 보입니다. 고양이와 강아지가 같은 주변 단어(“사료”, “먹었다”)를 향해 각각 끌려가는 겁니다. 고양이 벡터도 “사료” 쪽으로 이동하고, 강아지 벡터도 “사료” 쪽으로 이동하니까, 둘 다 비슷한 방향으로 움직이게 됩니다.

.

이걸 수억 번 반복하면:

.

“고양이”는 “사료”, “귀엽다”, “먹다” 쪽으로 계속 끌려감

“강아지”도 “사료”, “귀엽다”, “먹다” 쪽으로 계속 끌려감

“주식”은 “투자”, “상장”, “배당” 쪽으로 끌려감

.

결과적으로 같은 방향으로 끌려간 단어들의 벡터 수치가 비슷해지는 겁니다. 마치 두 사람이 각각 따로 출발했지만, 같은 목적지들을 향해 반복적으로 이동하다 보면 결국 비슷한 위치에 도달하는 것과 같아요.

.

Python 예제 코드

예제코드처럼 한글 임베딩 모델을 사용해야 좋은 결과를 얻을 수 있습니다.

from sentence_transformers import SentenceTransformer import numpy as np def cosine_similarity(vec1, vec2):     “””두 벡터의 코사인 유사도 계산”””     dot_product = np.dot(vec1, vec2)     norm1 = np.linalg.norm(vec1)     norm2 = np.linalg.norm(vec2)     return dot_product / (norm1 * norm2) # 임베딩 모델 로드 (한국어 특화 모델) model = SentenceTransformer(“nlpai-lab/KURE-v1”) texts = [     “고양이는 귀여운 반려동물이다”,     “강아지와 고양이는 사람들이 좋아하는 반려동물이다”,     “오늘 주식 시장이 크게 하락했다”,     “금융 시장의 변동성이 커지고 있다”, ] # 텍스트 → 임베딩 벡터 변환 embeddings = model.encode(texts) # 모든 텍스트 쌍의 유사도 출력 for i in range(len(texts)):     for j in range(i + 1, len(texts)):         sim = cosine_similarity(embeddings[i], embeddings[j])         print(f”{texts[i]}”)         print(f”{texts[j]}”)         print(f”유사도: {sim:.4f}”)         print()

.

두 문장의 유사도를 출력합니다.

유사한 두 문장은 유사도가 높고 관련 없는 두 문장은 유사도가 낮은것을 볼 수 있습니다.

고양이는 귀여운 반려동물이다 강아지와 고양이는 사람들이 좋아하는 반려동물이다 유사도: 0.8005 고양이는 귀여운 반려동물이다 오늘 주식 시장이 크게 하락했다 유사도: 0.3343 고양이는 귀여운 반려동물이다 금융 시장의 변동성이 커지고 있다 유사도: 0.3287 강아지와 고양이는 사람들이 좋아하는 반려동물이다 오늘 주식 시장이 크게 하락했다 유사도: 0.3696 강아지와 고양이는 사람들이 좋아하는 반려동물이다 금융 시장의 변동성이 커지고 있다 유사도: 0.3548 오늘 주식 시장이 크게 하락했다 금융 시장의 변동성이 커지고 있다 유사도: 0.5807